In our prior tutorial we looked at using an axis aligned bounding box to perform collision testing. One big downside was the handling of sprite rotation. Today, we will look at using a circle instead of a rectangle for our collision detection. The circle has the obvious advantage of being the same size no matter how much you rotate it. It is also extremely fast to calculate and test for collisions. Although as you can see from the application to the right, it isn’t extremely accurate.
Just the Math
Calculating the bounding circle radius:
function getBoundingCircleRadius(sprite){
return Math.sqrt(((sprite.image.width/2 * sprite.image.width/2)
+ (sprite.image.height/2 * sprite.image.height/2)));
}
Checking for an intersection between circles
function circlesIntersect(c1X,c1Y,c1Radius, c2X, c2Y, c2Radius){
var distanceX = c2X – c1X;
var distanceY = c2Y – c1Y;
var magnitude = Math.sqrt(distanceX * distanceX + distanceY * distanceY);
return magnitude < c1Radius + c2Radius;
}
Description
As mentioned earlier, a bounding circle removes the complexity of dealing with rotation. This is a bit of a double edge sword though. An axis aligned bounding box can be tighter and more accurate than a bounding circle, but as it rotates it quickly becomes less so. The following application illustrates the same shape bounded by both a bounding box and a bounding circle. As you can see, at some points the bounding box is a great deal more accurate, but as it rotates, it becomes a great deal less accurate:
The calculations for the bounding circle are however a great deal easier to perform. Let’s take a look at them now.
Math.sqrt(((sprite.image.width/2 * sprite.image.width/2)
+ (sprite.image.height/2 * sprite.image.height/2)));
First we start off by calculating the radius of our sprite’s image. This is a matter of calculating the length of furthest point from the centre, giving us the smallest possible radius that encompasses our sprite. The process is rather straight forward and is calculated using pythagorean theorem again. We are essentially calculating the magnitude (or distance) from the centre of our sprite to the corner, we do this by forming a right angle triangle.
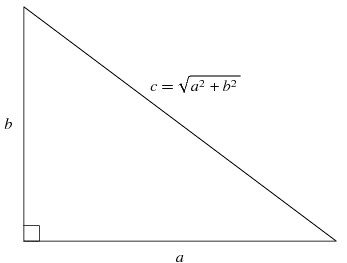
For a bit of a refresher on pythagorean theorem (which is used A LOT), consider this diagram I stole:
a is the X coordinate of our corner, b is the Y coordinate of our corner, therefore the distance or magnitude ( the second is the correct term mathematically ) between those two points is c, which you can calculate by taking the square root of the square of a plus the square of b. Or using our actual variable names, distance = square root( x * x + y * y). The resulting value of this equation is the distance between x and y. So, how did we come up with the values for x and y? That part was simple, since our pivot is at the centre of our sprite, x is simply half the width of the image, while y is half the height.
If that just confused the hell out of you, the following diagram might help a bit. It illustrates how pythagorean theorem is being applied to our actual jet sprite to calculate the distance to the corner.
So, now we have the distance to the corner, which we can now use it as our circle’s radius. Now we need to figure out how to determine if an intersection occurs.
var distanceX = c2X – c1X;
var distanceY = c2Y – c1Y;
var magnitude = Math.sqrt(distanceX * distanceX + distanceY * distanceY);
return magnitude < c1Radius + c2Radius;
This again is a simple and quick equation. Actually, its the exact same formula again, this time though, we calculate x and y by measuring the magnitude ( distance ) between each of our circles centre points. Once we have calculate the magnitude between the two circles, we simply check to see if that distance value is less than the total radius of both circles. If the magnitude is less than the radius of both circles combined, they intersect, otherwise they don’t.
One thing you should be aware of ( but not too concerned with initially ) is the square root operation is an expensive one and generally something you want to avoid. A square root is many times slower to perform than a multiplication or division. In this situation, it is a very easy to eliminate, you simply square both sides, like so:
function circlesIntersect(c1X,c1Y,c1Radius, c2X, c2Y, c2Radius){
var distanceX = c2X – c1X;
var distanceY = c2Y – c1Y;
var magnitudeSquared = distanceX * distanceX + distanceY * distanceY;
return magnitudeSquared < (c1Radius + c2Radius) * (c1Radius + c2Radius);
}
If you are still struggling with the math though, these kinds of optimizations can happen later if they are needed at all. It’s often easier to optimize after the fact anyways, so don’t worry too much about being fast quite yet. It’s far too easy to get caught up optimizing prematurely.
Complete Code
<!DOCTYPE html>
<html>
<head>
<script src=“http://code.createjs.com/easeljs-0.5.0.min.js”></script>
<script>
var jetSprite,jetSprite2;
var boundingCircle1, boundingCircle2;
var actualBounds;
var stage;
document.addEventListener(‘DOMContentLoaded’, demo,false);
function getBoundingCircleRadius(sprite){
return Math.sqrt(((sprite.image.width/2 * sprite.image.width/2)
+ (sprite.image.height/2 * sprite.image.height/2)));
}
function createBoundingCircle(sprite,useMaxExtents){
var g = new createjs.Graphics();
g.setStrokeStyle(2);
g.beginStroke(createjs.Graphics.getRGB(0,0,255));
var radius = getBoundingCircleRadius(sprite);
g.drawCircle(sprite.x,sprite.y,radius);
return new createjs.Shape(g);
}
function circlesIntersect(c1X,c1Y,c1Radius, c2X, c2Y, c2Radius){
var distanceX = c2X – c1X;
var distanceY = c2Y – c1Y;
var magnitude = Math.sqrt(distanceX * distanceX + distanceY * distanceY);
return magnitude < c1Radius + c2Radius;
// Note, sqrt is a slow operation, square both sides for better performance
// var magnitudeSquared = distanceX * distanceX + distanceY * distanceY;
// return magnitudeSquared < (c1Radius + c2Radius) * (c1Radius + c2Radius);
}
function demo(){
stage = new createjs.Stage(“theCanvas”);
jetSprite = new createjs.Bitmap(“jetsprite.small.png”);
jetSprite.regX = 30; // Half image width
jetSprite.regY = 40; // Half image height
jetSprite.y = 200;
jetSprite.x = 100;
jetSprite.image.onload = function(){
boundingCircle1 = createBoundingCircle(jetSprite);
stage.addChild(boundingCircle1);
}
stage.addChild(jetSprite);
jetSprite2 = new createjs.Bitmap(“jetsprite.small.png”);
jetSprite2.regX = 30; // Half image width
jetSprite2.regY = 40; // Half image height
jetSprite2.y = 200;
jetSprite2.x = 300;
jetSprite2.image.onload = function(){
boundingCircle2 = createBoundingCircle(jetSprite2);
stage.addChild(boundingCircle2);
}
stage.addChild(jetSprite2);
//And go…
stage.update();
// onFrame will be called each “tick”. Default is 50ms, or 20FPS
createjs.Ticker.addListener(onFrame);
}
function onFrame(elapsedTime) {
jetSprite.x++;
jetSprite.rotation = jetSprite.rotation+1;
stage.removeChild(boundingCircle1);
boundingCircle1 = createBoundingCircle(jetSprite);
stage.addChild(boundingCircle1);
stage.addChild(boundingCircle2);
if(circlesIntersect(jetSprite.x, jetSprite.y, getBoundingCircleRadius(jetSprite),
jetSprite2.x, jetSprite2.y, getBoundingCircleRadius(jetSprite2)))
{
jetSprite.x = 100;
}
stage.update();
}
</script>
</head>
<body>
<canvaswidth=400height=400id=“theCanvas”style=“background-color:black”/>
</body>
</html>
See Also
See Collision Detection using an axis-aligned bounding box for details on bounding boxes.
If you are still struggling with the use of triangles, you really need to wrap your head around this concept. This Youtube video ( with horrible audio ), gives a good example of pythagorean theorem in action: